Samuel Drews
Proving Data-Poisoning Robustness in Decision Trees
Dec 02, 2019

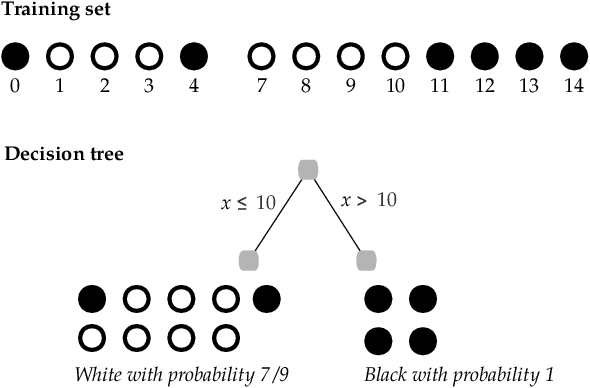
Abstract:Machine learning models are brittle, and small changes in the training data can result in different predictions. We study the problem of proving that a prediction is robust to data poisoning, where an attacker can inject a number of malicious elements into the training set to influence the learned model. We target decision-tree models, a popular and simple class of machine learning models that underlies many complex learning techniques. We present a sound verification technique based on abstract interpretation and implement it in a tool called Antidote. Antidote abstractly trains decision trees for an intractably large space of possible poisoned datasets. Due to the soundness of our abstraction, Antidote can produce proofs that, for a given input, the corresponding prediction would not have changed had the training set been tampered with or not. We demonstrate the effectiveness of Antidote on a number of popular datasets.
Quantifying Program Bias
Mar 07, 2017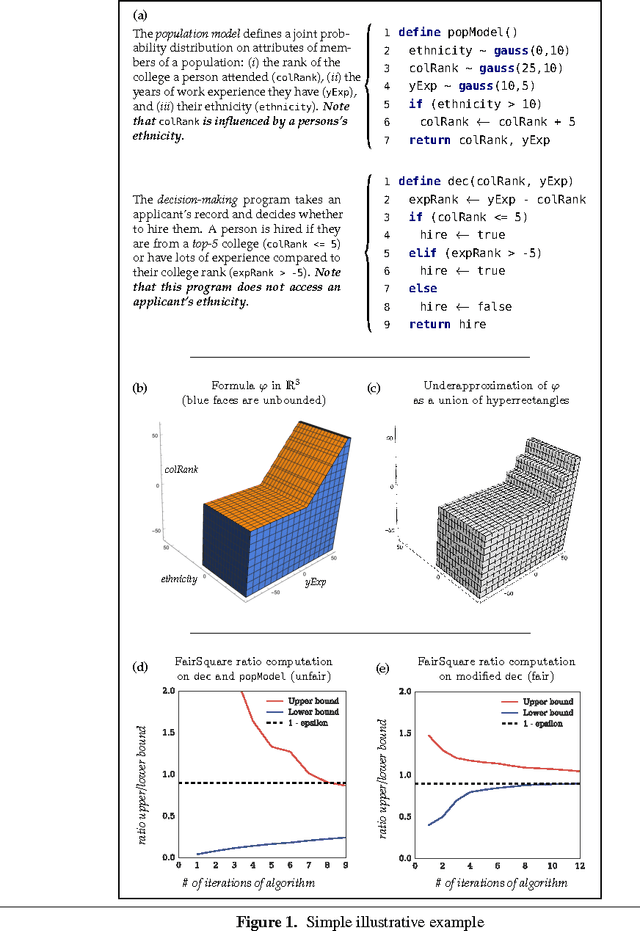
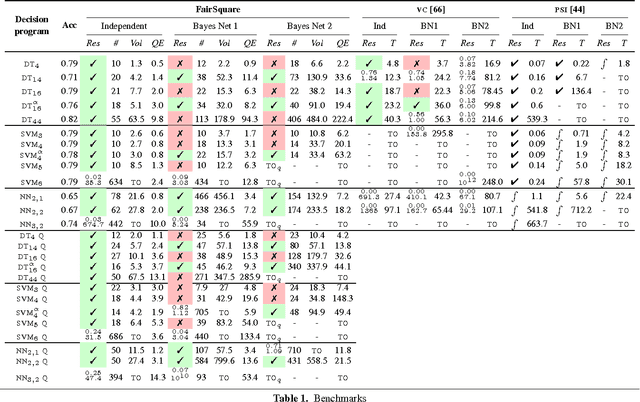
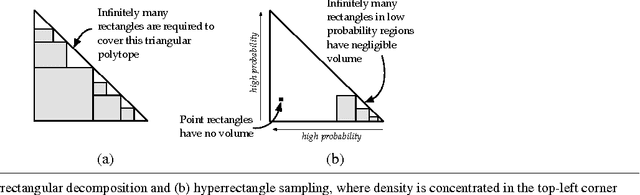
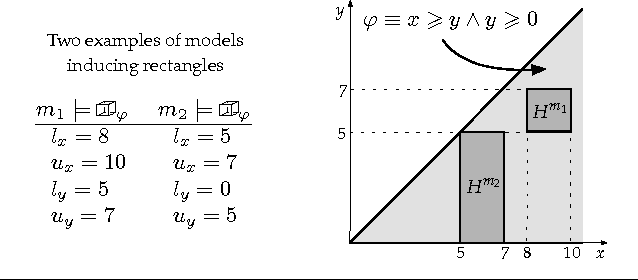
Abstract:With the range and sensitivity of algorithmic decisions expanding at a break-neck speed, it is imperative that we aggressively investigate whether programs are biased. We propose a novel probabilistic program analysis technique and apply it to quantifying bias in decision-making programs. Specifically, we (i) present a sound and complete automated verification technique for proving quantitative properties of probabilistic programs; (ii) show that certain notions of bias, recently proposed in the fairness literature, can be phrased as quantitative correctness properties; and (iii) present FairSquare, the first verification tool for quantifying program bias, and evaluate it on a range of decision-making programs.
Fairness as a Program Property
Oct 19, 2016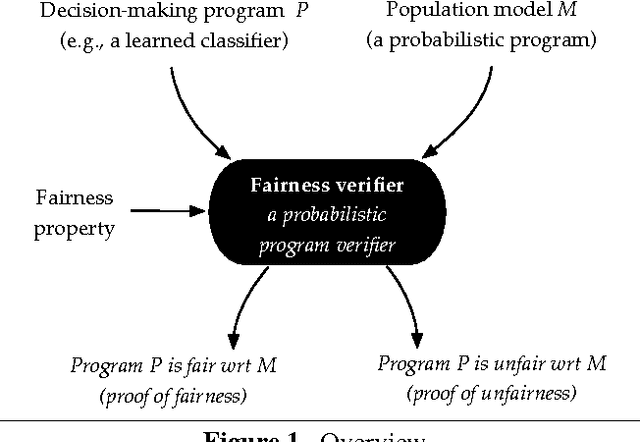
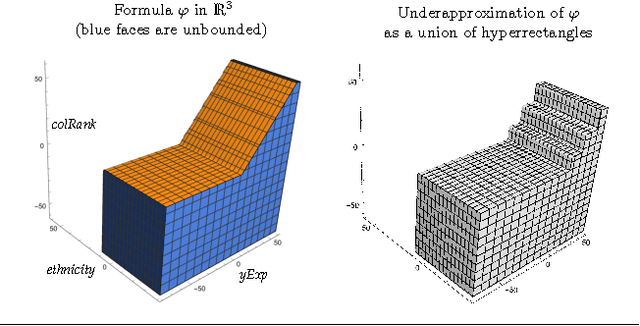
Abstract:We explore the following question: Is a decision-making program fair, for some useful definition of fairness? First, we describe how several algorithmic fairness questions can be phrased as program verification problems. Second, we discuss an automated verification technique for proving or disproving fairness of decision-making programs with respect to a probabilistic model of the population.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge